Why Singapore Math Olympiads ?
Part-2
Figure out the answers to the following two questions.
I) What is the next number in the series ?
46,44,42,40,38, ____
II) Few persons are sitting around a circular table. If the 3rd person is sitting exactly opposite to the 9th person, how many total persons are there ?
Let me tell you that both these questions are primary grade Olympiads (grade 2 or grade 3) level questions !
For question-(I), it can be easily deduced by a 2nd or 3rd grader that its back counting minus 2. So the series, 46 , 44 (=46-2), 42 (=44-2), 40 (=42-2), 38 (=40-2), 36 (=38-2). The answer turns out to be 36.
Its Easy huh !!
Now, for question(II), a 2nd /3rd grader may proceed by drawing a round table and putting “3” just opposite to “9”. Then the student may forward count from 3 to 9 and check that there are 5 students in between 3 and 9(see figure). Finally , the student may try to fit 5 students on the left side by both forward and back counting and should figure out that there are total 12 persons across the table.
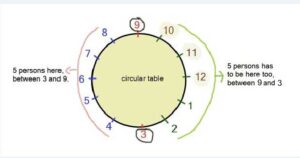
Though a much elder child may easily figure out that the total persons shall be (9-3)x2= 6×2 =12 , we need to understand how a 2nd or 3rd grader may proceed.
We notice that question(II), which is a typical South East Asian/Singapore Olympiad question also tests the concept of forward and back counting, but with a twist.
The Singapore math questions compel students to think beyond school syllabus and in turn increases logical bend of mind in true sense.
For more, on how to appear for these Olympiads visit Olympiads-For Champs.
Keep visiting my blog page for more such problems and discussion.
