The Magic Square - Global Math Olympiad.
Asked Where ? :
A typical question once asked in one of the Singapore Math Olympiads, meant for Grade-4 and Grade-5, but it can challenge an expert and grown-up Mathematician too. Please give it a try !!
If you think it’s too easy, take the “Reader’s Challenge“
The Problem :
We have a “Magic table” shown below, which gets filled up following certain rule. Try to figure out the rule and find out, at which row and at which column the number “2021” exists.

The Solution :
At first glance , the problem may seem too difficult, specially for a student of grade-4 or 5 , but solving such problems requires the real logical sense . A regular practice of such tricky mathematics only can prepare the potential little champs for the “REAL MATH OLYMPIADS”, winning where, gives you the real PRIDE.
Coming to the problem, a keen observation will lead us to the following facts about the “Magic table”
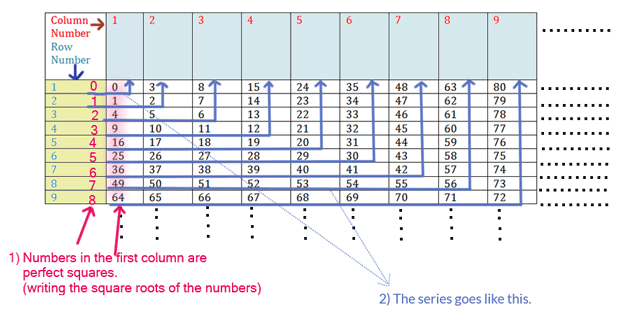
1) The numbers in the first column are the squares of consecutive whole numbers, staring with “0” ( Reminder: Whole numbers start with “zero” and natural numbers start with “1”) .
2) Row-wise the series starts with a perfect square and then get incremented by 1 towards right in every next column, till it takes a turn upwards.
The number where the series in a row takes turn = the number in the first column + √(the number in the first column )
For example, Take the 5th row :
The number in the first column = 16
The number where the series that 5th takes turn = 16 + √16 = 16+4 =20
3) The topmost number in a column = The number where the series in a row takes turn + √(the number in the first column )
For example, Take the series in the 5th row and 5th column :
The topmost number in the column = 20 + √4 = 24
Still confused ?? Please see the solution figure-1 below.
So,now if you have understood how the table is being populated , try to solve without reading further. If still confused , read further.
Now, it is understood that a series in a row starts with a perfect square , and then it gets incremented by 1 further across the consecutive cells , then takes a turn upwards at a number (which equals the sum of the initial number plus the square root of that initial number) and then ends at the top most row at a number(which equals the sum of number at which the series takes turn and the square root of the initial number). The next row starts with the next consecutive number , which is again a perfect square.

Following this rule, we first figure out that the perfect squares of two consecutive numbers between which 2021 lies. And by some simple checking , we notice that 2021 lies between 442 (=1936)and 452 (=2025).
So, the 45th row starts with square of 44, equaling 1936 and then get incremented in every consecutive cells rightwards by “one” till 1980(=1936+44) and then turn upwards and ends at the topmost row at 2024 (=1980+44). Counting some cells backwards , we may easily find that the number “2021” lies at the 4th row and 45th column. Please understand the calculations done over the table below for more clarity.

Huh !! I hope I have been able to explain the solution. If you have any easier approach to the problem , please let me know in the comment section. I will definitely add that to this blog.
The Answer :
The number “2021” lies at the 4th row and the 45th column.
The Reader’s challenge :
What will be the 99th term of the following series, which follows a certain rule.
1, 2, 3, 4, 10, 5, 6, 7, 8, 26, 9, 10, 11, 12, 42………
Expert’s challenge:
Find out a general formula for finding the nth term of the given series.
